为何不能躺平,因为网络模型在疫情预测上存在测不准
近来外媒(例如WSJ,纽约时报)不断炒作,说国内的清零是不可持久的。但严肃的学术期刊上,却给出了相反的建议。今天介绍的论文,来自PNAS,标题是“使用网络模型对疫情传播进行有效预测的本质缺陷”,用一句话概括,就是从计算复杂性理论出发,就别指望能有一个有效预测疫情传播的算法。而既然不存在一般性的预测模型,那若是面对疫情躺平任X,那就必须要面对未知的未知这最坏的不确定性。

论文地址:https://www.pnas.org/content/119/4/e2109228119#abstract-2
论文摘要:新冠大流行强调了发展可靠的疾病预测模型的重要性,这将使决策者制定适当的应对策略。尽管最近有很多关于这个话题的研究,但是对于流行病的预测仍然知之甚少。研究人员将预测传染动态的困难归因于多种因素,包括复杂的行为反应、数据的不确定性、潜在过程的随机性,以及疾病参数对环境变化的高度敏感性。该研究提供了一个严谨的,对使用网络模型预测感染人数的计算复杂性的分析。
具体来说,我们展示了几个预测问题(例如,在给定时间至少有一定数量的人被感染的概率和感染人数在给定时间达到高峰的概率)是难以计算的。例如,这些问题的有效解决意味着在合取范式中任意布尔公式的满意赋值的数量可以被有效计算,这违背了计算复杂性的一个广泛认同的假设。即使在所有疾病参数都已知且假定对环境变化不敏感的理想情况下,这种棘手的结果仍然适用。从计算复杂性的观点出发,我们的研究结果表明,传染动力学变得不可预测这一性质,给预测疾病传播,带来了一些根本的困难。在积极的一面,我们可发展在受限条件下的有效近似算法解决预测问题。
*********************简要概述全文精华*****************************
使用最常见的SIR模型,对下面这个网络中的传播情况进行预测,最初的感染者是v0,下图展示了一种可能的传播方式:
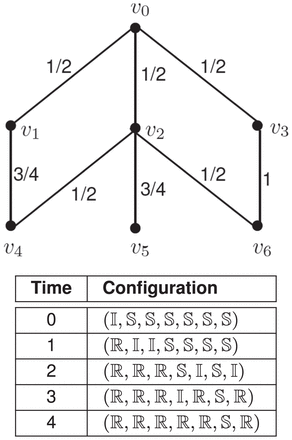
在上述网络上,要求解以下四个问题,都是NP难的,也就是当问题涉及的节点数增长时,所需的计算复杂度会以指数级增加,这在工程上,意味着问题是不可解的。
计算在 t 时节点的一个给定子集 s 中新感染的数目至少为 q 的概率。计算节点子集 s 中感染总数至少为 q 的概率。计算子集 s 中节点在时间 t 时的脆弱性(即子集 s 中所有节点在时间 t 时受到感染的概率)。PR-INF-BY (t,s)用时间 t 计算 s 中节点的脆弱性(即 s 中所有节点被时间 t 感染的概率)。
而将传播模型从SIR改为SI,或者SIS,同样是不可解的。
这意味着,短期来看,即使完全知道系统的初始状态,且疾病的传播规律不变(没有变异株)疾病的传播具有广泛的不可预测性。这不仅针对个体,也适用于集体属性。预测过程中,任何一个变量的改变,都会使得模型变得不可预测。只有在某些特殊情况下,才可以由网络模型得出有效地预测。
对此的应对方式,文中给出的建议,除了找出近似算法,或满足特定假设的启发式方法外,值得注意的是第二条,对接触网络进行结构限制,例如当社会联系网络具有固定的连接数。用人话来说,就是国内采取的干预措施,例如封闭小区等,在这种情况下,模型是具有可预测性的。
从该研究中,得出的结论很清晰,那些预测如果放任病毒传播的人,他们对可能感染数的预测都是在胡扯,不可相信,对于今年结束流行的说法,也要保有怀疑。且不说新冠的后遗症,单就目前的病死率和重症率,就绝不能听之任之。面对疫情,只要清零和大流行两种选择,没有中间地带。
更多阅读